Blob detection is a task that identifies and localizes regions in an image which stand out in terms of intensity, texture, or other properties, often representing features or objects of interest. To detect the blobs, various methods such as Difference of Gaussians (DoG) or Laplacian of Gaussian (LoG) are used to identify regions with significant intensity changes or distinct shapes across different scales.

There are 2 key concepts in blob detection task:

1. Scale Invariance: Blobs can exist at various scales. A robust blob detection method identifies blobs regardless of their size.
2. Feature Detection: Blobs are identified by local maxima or minima in some measure of intensity or contrast, often involving gradients or second-order derivatives.

When detecting blobs, 2 common methods are used: Laplacian of Gaussian(LoG) and Difference of Gaussian(DoG).

1. Laplacian of Gaussian (LoG)

The Laplacian of Gaussian method combines Gaussian smoothing with the Laplacian operator to detect blob-like structures.

Steps:

1. Convolve the image with a Gaussian kernel to smooth it and reduce noise.
2. Apply the Laplacian operator to detect regions where the intensity changes significantly.
3. Identify the zero-crossings or extrema (local maxima or minima) of the resulting image to detect blobs.
4. Repeat the process at multiple scales by varying the standard deviation ((\sigma)) of the Gaussian kernel.

Although they give accurate results, they are computationally expensive to implement.

This is where Difference of Gaussian comes in.

2. Difference of Gaussians (DoG)

DoG is an approximation of LoG that is computationally more efficient.

Steps:

1. Create two versions of the image by smoothing it with Gaussian filters of different standard deviations \(\sigma_1\) and \(\sigma_2\).
2. Subtract the two smoothed images (\(DoG = G_{\sigma_1} - G_{\sigma_2}\)) to highlight areas where intensity changes.
3. Detect local extrema in the resulting image.
4. Downsample the image instead of increasing kernel size for better efficiency.

DoG is faster than LoG while providing similar results.

Implementation Details

Kernel Size & Sigma

In the implementation, the kernel size is dynamically adjusted based on the value of sigma to ensure that the Gaussian filter captures sufficient image area for accurate blob detection. The kernel size is computed as:

This formula ensures that the kernel size is large enough to encompass the main extent of the Gaussian distribution. Specifically, the value \(3 \times \sigma\) corresponds to approximately three standard deviations of the Gaussian, which covers over 99% of the distribution.

At each iteration, the value of sigma is multiplied by a factor \(k\) which is a configurable parameter. As a result, the kernel size also increases proportionally with \(k\). Consequently, the outcomes are influenced by the initial value of sigma that is chosen.

Number of Iterations

The number of iterations in blob detection refers to the number of scales or levels processed by the algorithm during its execution. Iterations are crucial in scale-space representations, as they allow the algorithm to detect blobs of various sizes by progressively increasing the scale of analysis.

Role of Iterations in Blob Detection

1. Scale-Space Construction:
   • Blob detection algorithms, like Difference of Gaussians (DoG) or Laplacian of Gaussian (LoG), analyze the image at multiple scales to ensure blobs of all sizes are captured.
   • Each iteration corresponds to analyzing the image at a specific scale determined by the scaling factor \(k\) and the initial sigma.
2. Blob Size Coverage:
   • Increasing the number of iterations ensures that a wider range of blob sizes is analyzed.
   • Fewer iterations might result in missed detections for blobs that do not align with the analyzed scales.
3. Accuracy vs. Computation Trade-off:
   • More iterations improve the precision of blob detection by providing a finer scale-space resolution.
   • However, each iteration adds computational cost, as more image smoothing, convolution, and extrema detection operations are performed.

Impact of the Number of Iterations

Small number of iterations enables faster processing and lower computational load. However, there is a risk of missing blobs, especially those at scales not analyzed during the limited iterations. On the other hand, too many iterations can have more comprehensive detection of blobs across a broad range of sizes However, it can cause higher computational cost and potentially redundant or overlapping blob detections.

Factor \(k\)

The scaling factor \(k\) had a significant impact on the blob detection process. After conducting several trials, the best results were obtained with a scaling factor of \(k = 1.3\). This value provided the most accurate detection across various blob sizes, particularly in capturing the appropriate blob structures within the image. When the scaling factor deviated from 1.3, the algorithm struggled to properly detect blobs, either failing to capture important features or generating erroneous blob detections.

Why is \(k\) Important?

The scaling factor \(k\) determines the rate at which the scale changes across iterations in the blob detection algorithm. It affects:

1. Scale Resolution: Smaller values of \(k\) increase the scale resolution, allowing the algorithm to detect blobs with finer detail and less overlap. However, this comes at the cost of increased computational time since more iterations are required.
2. Detection Accuracy: Larger values of \(k\) may result in missed blob structures, as the algorithm skips over intermediate scales that might contain critical information.
3. Efficiency: \(k\) provides a balance between computational efficiency and the precision of blob detection. A well-chosen \(k\) ensures that the algorithm is both effective and fast.

Threshold

The threshold is a critical parameter in blob detection algorithms. It determines the minimum or maximum intensity value that qualifies as a blob, thereby affecting both the sensitivity of the detection and the quality of the results.

Role of Threshold in Blob Detection

1. Blob Identification:
   • Thresholding is used to filter out insignificant regions or weak responses from the blob detection algorithm.
   • For instance, in methods like Difference of Gaussians (DoG) or Laplacian of Gaussian (LoG), only regions where the intensity response exceeds the threshold are considered as potential blobs.
2. Noise Reduction:
   • A well-chosen threshold helps eliminate noise or irrelevant features in the image, ensuring that only meaningful blob structures are detected.
3. Detection Sensitivity:
   • A lower threshold increases sensitivity, allowing the detection of faint or smaller blobs. However, this might result in false positives.
   • A higher threshold reduces sensitivity, focusing on stronger or more prominent blobs but potentially missing smaller or less distinct ones.

Impact of Threshold on Results

Low Threshold captures more blobs, including faint or small structures but it may detect noise or irrelevant regions, resulting in false positives. High Threshold reduces false positives by focusing only on blobs with strong responses but may miss subtle blobs or important features with lower intensity.

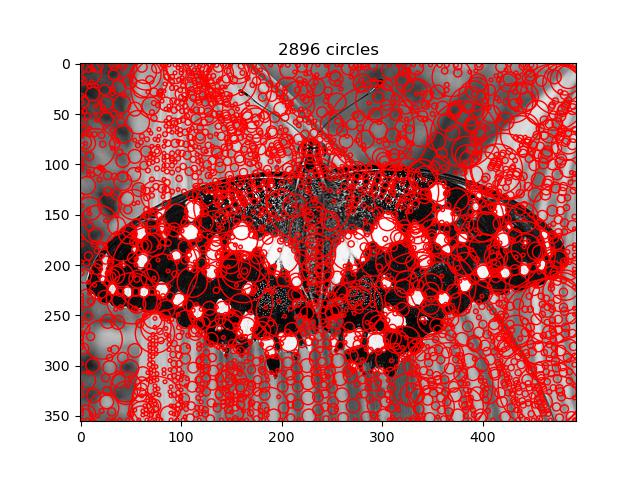
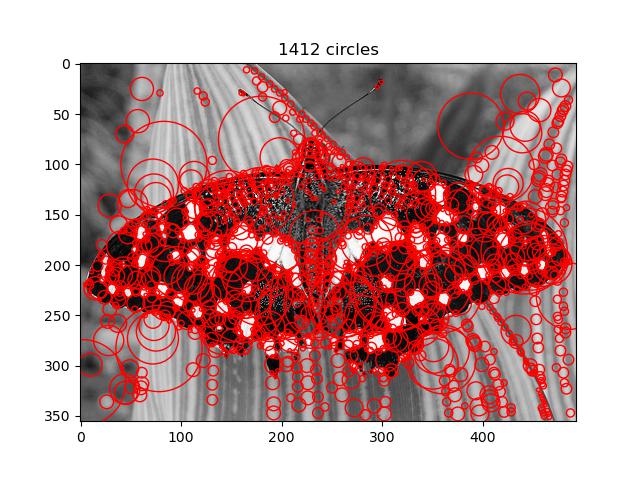
Colorized Outputs with Blobs

Displayed are best results.

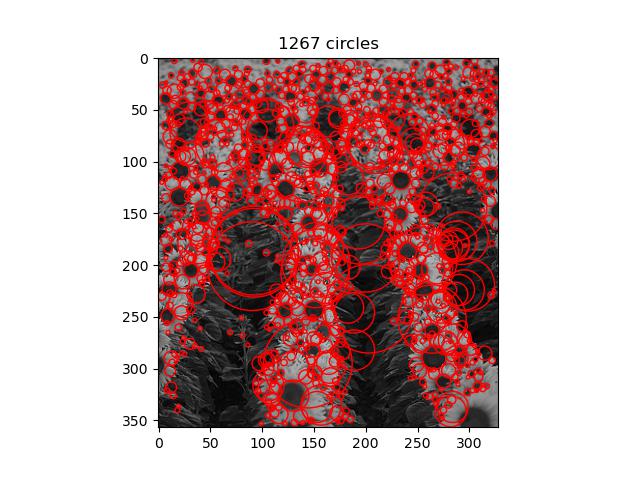
Check out the code here!